Hands on IA: Modelos de Clasicación
¿Sabías que muchas decisiones del día a día —desde detectar spam hasta predecir si va a llover— se basan en clasificar información?
La clasificación es una de las tareas más comunes en Inteligencia Artificial. A diferencia de los modelos de regresión, que predicen un número, los modelos de clasificación buscan responder preguntas del tipo: ¿Esto pertenece a la categoría A o a la B?
Algunos ejemplos de cuando aplicamos esto en nuestro día a día:
- Cuando segmentas carteras de clientes
- Cuando defines si un crédito es riesgoso o no.
- Cuando tu celular predice si un mail es spam o no.
Si lo prefieres, puedes escuchar el podcast de este post:
Este post es el segundo de la serie "Hands on IA", aquí puedes encontrar el primer post:

Cómo operan los modelos de clasificación
Imaginemos que tenemos identificados días en que llovió (azules) y días en que no llovió (rojos), donde observamos además la temperatura y la presión, como en el gráfico que mostramos un poco más abajo. Así como en la regresión lineal encontramos una línea que predecía el valor de un punto, nos gustaría encontrar una forma de poder predecir si un nuevo punto observado (humedad,presión) debería ser un día con o sin lluvia:
Ejemplo: Frontera de decisión que separa los días con y sin lluvia en base a presión y humedad.
Intuitivamente el gráfico nos muestra que a menor presión y menor humedad es menos probable que llueva, a mayor presión y mayor humedad es más probable que llueva, por lo tanto podríamos pensar en algunas formas de predecir si un nuevo punto sería o no un día con lluvia:
- Vecinos, otra forma de predecir es utilizando los puntos que tengo cerca, si la mayoría de los puntos que tengo cerca son rojos (sin lluvia), podemos predecir que ese punto también debería ser un día sin lluvia, pero si la mayoría de los puntos cercanos son azules (lluvia), debería ser un día lluvioso. Este tipo de algoritmos usan los "vecinos" para determinar la clasificación de un nuevo punto.
- Una línea, ¿podemos encontrar una línea que separe los datos en lluviosos y no lluviosos? Si esa línea existiera, podríamos decir entonces que arriba de esa línea son días soleados y abajo de esa línea son días lluviosos. Esa línea sería nuestra "frontera de decisión", y la podríamos definir matemáticamente como:
\[ \text{Predicción} = \begin{cases} 1 & \text{si } w_0 + w_1 x_1 + w_2 x_2 \ge 0 \quad (\text{Llueve}) \\ 0 & \text{si } w_0 + w_1 x_1 + w_2 x_2 < 0 \quad (\text{No llueve}) \end{cases} \]
En este caso tenemos un modelo muy parecido a la regresión lineal, con dos variables (x1: humedad y x2: presión), pero con una diferencia importante, no queremos la mejor línea que pase por los puntos, queremos la mejor línea que separe los puntos, ya veremos esto en detalle más adelante.
Estos algoritmos usan "data etiquetada", es decir, ya tengo la información de cada punto observado y se si es o no un día lluvioso ("la etiqueta"), por esto se llaman "algoritmos supervisados".
Algoritmos Supervisados: Son un tipo de inteligencia artificial que aprende a partir de datos previamente etiquetados. Su objetivo es encontrar patrones en esos datos para poder predecir correctamente la etiqueta de nuevos casos que aún no han sido clasificados.
Ejemplos de Modelos Supervisados de Clasificación
Partamos revisando algunos ejemplos de algoritmos que clasifican en base a los valores de los vecinos:
K-NN (K-Nearest Neighbors – K Vecinos más Cercanos)
Es un algoritmo de clasificación supervisado que asigna una clase a un nuevo dato basándose en las clases de sus K vecinos más cercanos. La cercanía se mide con una métrica de distancia, como la distancia euclidiana. La predicción se realiza por mayoría de votos: el nuevo dato se clasifica según la clase más común entre esos vecinos.
Es un modelo simple, efectivo y no requiere entrenamiento previo: todo el conocimiento está en los datos, pero requiere calcular la distancia a todos los puntos en cada predicción, lo que puede ser poco eficiente.
Weighted K-NN (K-Vecinos Ponderados)
Es una variante del K-NN que asigna pesos a los vecinos según su distancia: cuanto más cerca está un punto, mayor es su influencia en la clasificación. Esto permite que los puntos más próximos tengan más impacto que los lejanos.
Es más certero cuando la cercanía importa más que la cantidad y reduce el impacto de outliers (puntos alejados) pero, sigue siendo ineficiente para muchos puntos.
Radius Neighbors (Vecinos dentro de un radio fijo)
En lugar de buscar un número fijo de vecinos, este algoritmo considera todos los puntos que se encuentran dentro de un radio determinado. Clasifica según la mayoría dentro del área.
Es más flexible pero depende del radio utilizado, pero si no hay datos en el radio no puede clasificar.
Estos son modelos básicos pero útiles para entender el concepto, los cuales veremos a continuación en una demo. Otros algoritmos en esta familia, más complejos son Ball Tree, KD-Tree, Approximate Nearest Neighbors, Edited Nearest Neighbor, Condensed Nearest Neighbor y Nearest Centroid Classifier. En general estos algoritmos tratan de hacerse cargo del problema de eficiencia, sin tener que recorrer todo el set de datos cada vez.
Prueba la demo: elige el algoritmo a probar, la cantidad de clases en el canvas, la cantidad de puntos en el canvas y la cantidad de vecinos o el radio (según el algoritmo que elijas) y añade nuevos vecinos con un click para ver como se clasifican:
🎯 Demo: Algoritmos de Vecinos
📌 Haz clic en el gráfico para agregar un nuevo punto y ver cómo se clasifica.
La segunda forma de clasificación de la que hablamos era la de encontrar "la mejor" recta que clasifique a los puntos, entendiendo que no todas las rectas que los separan son igual de buenas, hay algunas que discriminan mejor, las que maximizan la distancia entre los puntos y la recta.

El algoritmo que nos permite encontrar esta línea (o líneas si queremos clasificar varios tipos de datos) lo conocemos como SVM (Support Vector Machine o Máquinas de Vectores de Soporte). SVM permite encontrar las líneas (o fronteras) que mejor separa las clases, dejando el mayor margen posible entre los datos.
Este “margen” se define como la distancia entre la línea (o hiperplano) de separación y los puntos más cercanos de cada clase. Estos puntos se llaman vectores de soporte, y son cruciales, ya que son los que determinan directamente la posición de la frontera de decisión.
Prueba la demo: Elige la cantidad de clases, la cantidad de puntos y podrás ver las líneas o fronteras que mejor separan cada clase, arrastra los puntos con el mouse y verás como van cambiando estas fronteras.
🧠 Demo SVM Lineal Multiclase
📌 Puedes arrastrar los puntos con el mouse y ver cómo se mueven las fronteras.
Como puedes ver en la demo, a medida que aumenta la cantidad de clases, también lo hace la cantidad de clasificadores binarios necesarios (las líneas en el gráfico). Esto puede incrementar la complejidad del modelo y el tiempo de cómputo, especialmente en datasets grandes. Si trabajas con muchas clases o datos que no son linealmente separables, conviene considerar otros algoritmos como SVM con kernels, Random Forest o Redes Neuronales.
¿Datos no linealmente separables?
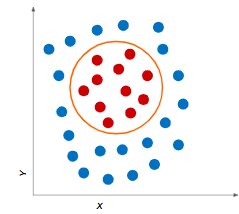
Si te fijas en la demo, siempre obtenemos líneas que intentan dividir las distintas clases presentes en nuestros datos, pero esto no siempre es posible, para este tipo de problemas veremos otros algoritmos más adelante.
Modelos de clasificación no supervisados
No siempre contaremos con datos etiquetados ¿qué hacemos en estos casos?, podemos tomar la data y tratar de buscar patrones o anomalías en ella.
Este tipo de algoritmos se conoce como "No Supervisados", son algoritmos donde se exploran los datos sin conocer las respuestas correctas. El objetivo principal es descubrir patrones, estructuras o relaciones escondidas en los datos. Esto lo hace útil en contextos donde no se dispone de etiquetas, o donde se busca explorar los datos antes de clasificarlos.
Este tipo de algoritmos son muy utilizados en segmentación de clientes, análisis de patrones de comportamiento, detección de anomalías, detección de fraudes y reducción de dimensionalidad.
Aquí encontramos algoritmos de clustering como K-Means, K-Means++ y DBSCAN, que agrupan datos en "clusters", donde los puntos agrupados en el mismos cluster presentan similitudes entre ellos:
K-Means: Agrupa por cercanía a centros, funciona de la siguiente manera:
- Eliges un número de grupos 𝐾
- El algoritmo ubica K puntos llamados centroides (uno por cada grupo).
- Cada dato se asigna al centroide más cercano.
- Luego, el centroide se ajusta al promedio de los puntos asignados.
- Repite hasta que los grupos ya no cambian.
K-Means++: Similar al anterior, pero mejora la elección inicial de los centroides. En lugar de elegirlos completamente al azar, lo hace de forma más estratégica para evitar que todos los centros partan muy juntos y reducir la posibilidad de que el algoritmo termine en una mala solución.
Prueba la demo: Elige el modelo, la cantidad de clusters y la cantidad de puntos, puedes elegir el delay para ir viendo como avanza el algoritmo o bien ir paso a paso ejecutándolo.
🧩 Demo Clustering K-Means
Veamos ahora DBSCAN.
DBSCAN: Agrupa por densidad, sin saber cuántos grupos hay. A diferencia de K-Means, no necesitas decirle cuántos grupos hay y puede detectar formas de grupos más irregulares. Funciona de la siguiente manera:
- Recorre los datos y busca regiones densas: zonas donde hay muchos puntos cercanos.
- Agrupa automáticamente esos puntos densos como un cluster.
- Puntos aislados o en zonas poco densas se consideran anómalos o ruido.
Prueba la demo: Elige la cantidad de clusters y la cantidad de puntos, puedes elegir el delay para ir viendo como avanza el algoritmo o bien ir paso a paso ejecutándolo. Para DBSCAN Eps es el radio del círculo donde se buscan las coincidencias y Min. Pts. es el mínimo de puntos que debe encontrar para asignar la coincidencia a una clase.
🔍 Demo DBSCAN
DBSCAN es un algoritmo poderoso para identificar agrupaciones de datos sin necesidad de definir cuántos grupos hay. A diferencia de otros métodos, también detecta puntos atípicos (ruido), lo que lo hace ideal para analizar datos con formas irregulares o presencia de valores fuera de lo común.
Conclusión
En este post exploramos cómo los algoritmos de clasificación y agrupamiento permiten que una máquina tome decisiones basadas en patrones. Aprendiste cómo distinguir clases con fronteras lineales (SVM), cómo clasificar usando los vecinos más cercanos (K-NN, Weighted, Radius), y cómo descubrir grupos ocultos sin etiquetas mediante clustering (K-Means, K-Means++, DBSCAN).
Cada uno de estos enfoques muestra una perspectiva diferente sobre cómo una IA puede "entender" los datos: ya sea buscando límites, vecindarios o densidades.
Y esto es solo el comienzo. En el próximo post vamos a dar un paso más: pasamos del clustering al mundo de la clasificación supervisada, empezando por uno de los modelos más sencillos y fundamentales: el Perceptrón. ¿Puede una neurona artificial aprender a distinguir dos clases? Lo vas a ver en acción.
¡No te lo pierdas! Vas a empezar a entender cómo aprenden las máquinas, literalmente.